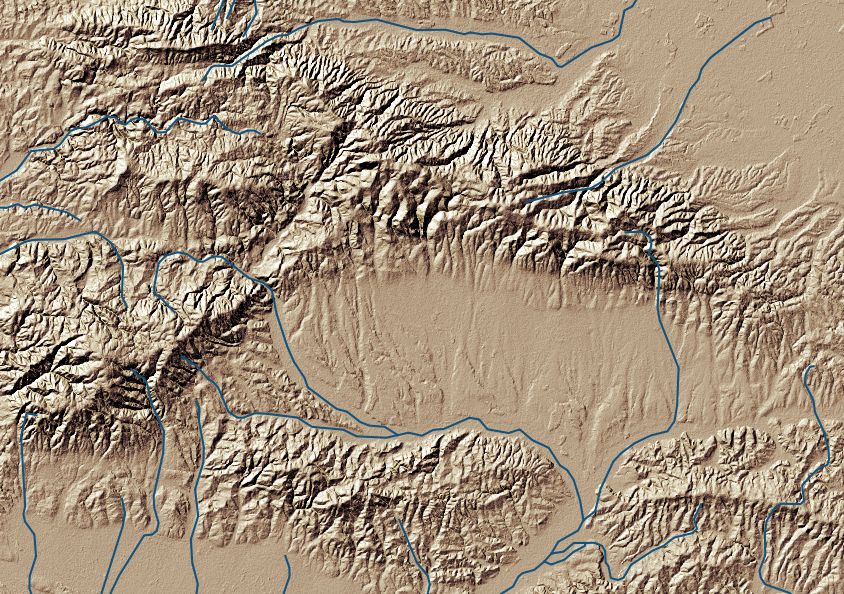
Figure 1. Hillshade model of Požega valley (Croatia).
Hillshade modelling is a standard form of terrain representation in cartography. The idea is to simulate light reflectance form a terrain surface, when illuminated from a specific direction (or multiple directions). The method is well known and constantly improved in GIS as a means of terrain visualisation. The basic principles of the hillshade method are quite simple (see below), but understanding and handling the outputs produced is less so.
The basics
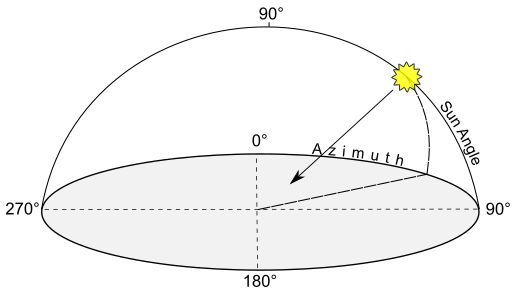
Figure 2. When calculating a hillshade we need to specify the sun direction (azimuth) and sun height, in angular units.
In a nutshell, hillshade algorithm assigns a theoretical reflectance value to each terrain element (a pixel of a digital terrain model in most cases). Given a defined light source, such reflectance will depend on the inclination of each terrain element: those that are perpendicular to the light source will receive and thus reflect more light than those that are facing other directions (see Fig. 3). In GIS, hillshade algorithms normally do not aim to model truly realistic scenes; factors such as surface texture or various light qualities are not taken into account. For this reason the immediate output is rather artificial and usually needs additional treatment in order to provide a visually pleasing terrain representation.
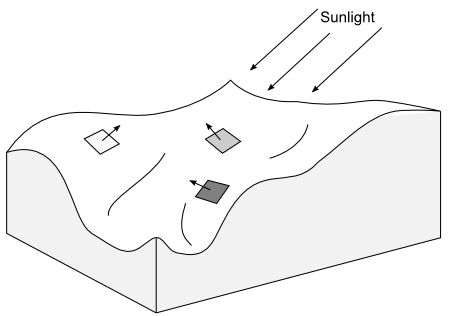
Figure 3. Surface reflectance (i.e. luminance) depends on the angle of incidence of sun rays.
The formula commonly used is the one devised by the mathematician Johan Heinrich Lambert, which postulates that the reflectance value will vary according to the difference between illumination angle and surface angle (Fig. 3). More specifically the amount of the reflected light will be proportional to the cosine of such angular difference (see on Wikipedia).
To understand the principle, imagine putting a piece of paper in front of a table lamp. The shadow of the paper on the table below will contract as you rotate or incline it, because you’re increasing the angular difference between the surface orientation and the light source. Now, the size of the shadow corresponds to the amount of light received by the paper, it will therefore appear darker when capturing diminishing amounts of light.
Hillshade implementation in Terrain Shading module for QGIS
Such simple approach has proven to be useful in GIS, but it certainly has some drawbacks. Hillshades often look rather artificial, and cannot be used to modelling complex, real-life lighting scenarios. (Ambient occlusion is one of those: see my previous post).
The Terrain Shading module, developed for QGIS, features a lambertian hillshade algorithm, but with an important modification. It enables to artificially exaggerate the angle of surface elements, i.e. pixels (Figure 3). This can be done in two directions, along the axis of illumination (longitudinal axis) and perpendicular to the illumination axis (lateral axis : Figure 4). These parameters enable us to adjust light quality, and to render more detail than with the standard cosine-law formula.
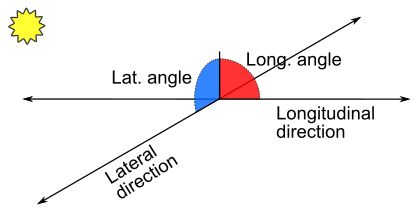
Figure 4. Surface orientation can be broken down to two angles (or vectors): longitudinal, parallel to the sun direction, and lateral, perpendicular to sun rays. Terrain Shading module for QGIS provides separate adjustments for these two angles.
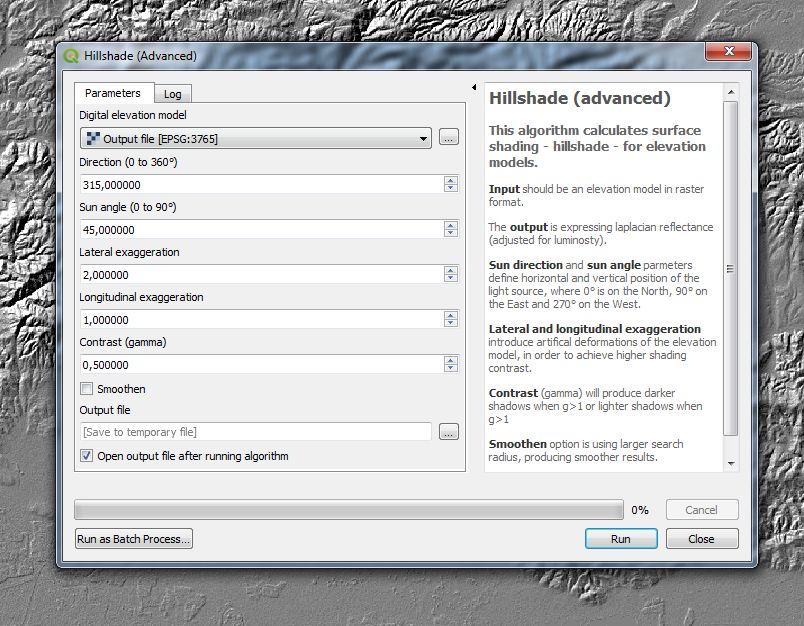
Figure 5. Terrain shading module for hillshade analysis. Note two settings for angular exaggeration.
Lateral exaggeration will accentuate slopes which may be poorly rendered with standard lambertian hillshade – as when overlying a hillshade model with a slope model. Such effect may be useful for the detection and visualisation of faint terrain features that are poorly visible in standard hillshade models. This approach may also prevent the appearance of washed out, highly illuminated slopes – a frequent, undesired effect (see the comparison of images below).
Figure 6. Comparison of standard hillshade model with the one with lateral angle exaggeration (factor: 3.0, very strong).
PS For a follow up, see the post on combining hillshades.
Bibliography
Article on Lambert’s cosine law on Wikipedia.
B. K. Horn 1981: Hill Shading and the Reflectance Map. Proceedings of the IEEE 69(1), 14-47. (download).